Using the same notation as last time we want to show that for

,

(where A is natrual number larger than 1) maximized at the second crossings. Why?
Definition. Let

be the largest integer that

.
The above claim is equivalent to claiming that

is the global maximum of f.
Theorem.

.
Proof.

, the result follows.
Theorem.

iff

.
Proof. Straightforward by direct expansion.
Theorem.
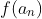
maximized at

.
Proof. This is equivalent to

.

which can be shown using modular arithmetic. (It isn't hard to check: there are only finite case to check.)
How about the case

?
Note that

and let

. Consider the case

which is larger than zero for large enough a_k. Now we can summarize our approach to find our optimal solution:
Check the following value of a: if they are a better solution replace the current one.
1) The

(usually the best answer)
2) Find smallest

. For each

find

so that

is maximized in the range

.
Complexity? Something like

. The problem is how often the answer falls on

and how should we make the algorithm more efficient? I would leave that part open.
What about irrational case? Let's talk about them next them.








No comments:
Post a Comment